
Stretching a graph means to make the graph narrower or wider. They are caused by differing signs between parent and child functions.Ī stretch or compression is a function transformation that makes a graph narrower or wider. Reflections are transformations that result in a "mirror image" of a parent function. have a rotation about any point, reflection over any line, and translation along any vector. Reflection of point using graph paper is described as a figure that is built around a single point. Graphing Dilations Dilations can be performed on a coordinate plane. Reflecting a graph means to transform the graph in order to produce a "mirror image" of the original graph by flipping it across a line. The line of reflection is a line along which an image reflects. Reflections are congruence transformations that generate a mirror image of an object, without changing its size or shape. Practice this lesson yourself on right now. All other functions of this type are usually compared to the parent function. 0:00 / 4:57 Determining the line of reflection Transformations Geometry Khan Academy Fundraiser Khan Academy 7.66M subscribers 70K views 7 years ago Transformations Geometry Khan. What is the position of the reflected shape: A, B, C or D Reflection in x -y Question. 70K views 7 years ago Transformations Geometry Khan Academy. Sketch the graph of each of the following transformations of y = xĪ stretch or compression is a function transformation that makes a graph narrower or wider, without translating it horizontally or vertically.įunction families are groups of functions with similarities that make them easier to graph when you are familiar with the parent function, the most basic example of the form.Ī parent function is the simplest form of a particular type of function. The equation of the resulting parabola is. Graph each of the following transformations of y=f(x). vertex the turning point of a parabola the minimum or maximum point on the parabola reflect over the x-axis and shift down 5 Which of the following describes the transformation of the graph y x2 in graphing y -x2 - 5 y (x + 7)2 The graph of y x2 has been translated 7 units to the left. The fixed line is called the line of reflection. reflection flipping a pre-image over a certain line in the coordinate plane (called the. Let y=f(x) be the function defined by the line segment connecting the points (-1, 4) and (2, 5). A reflection maps every point of a figure to an image across a fixed line. Unit 1: TransformationsReflections Objective: To learn to identify, represent, and draw the reflections of figures in the coordinate plane. Then you only need to put \(x\) into \(s(x)\) or \(g(x)\) and you're done. As \(s\) and \(g\) have exactly point in common, the following equation gives exactly one result: Reflections in the x-axis If (f (x) x2), then (-f (x) - (x2)). So you simply put in the values \(x,y\) of P and solve to \(t\): Reflections of graphs Graphs can be reflected in either the (x) or (y) axes.
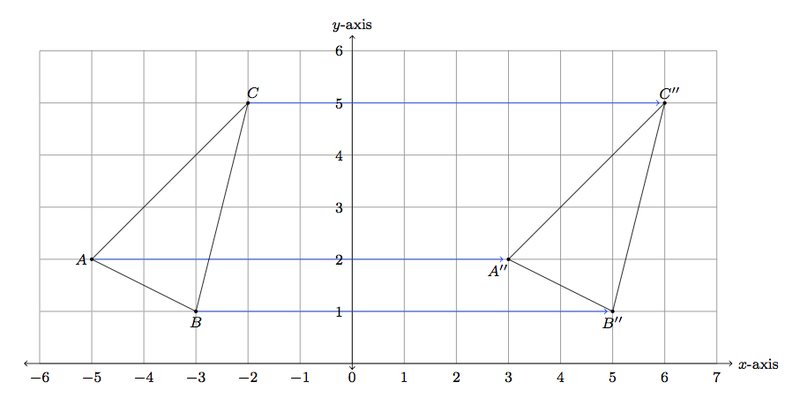
You have to know this: \(m_s = - \frac\)Īnd then you know that \(P\) is on \(s\). Reflection over the line y -x A reflection in the line y x can be seen in the picture below in which A is reflected to its image A. Double the length of the perpendicular in the direction of $L$.įirst you have to get the perpendicular \(s(x) = m_s \cdot x + t\) (the dashed red line). Reflections take a parent function and provide a mirror image of it over either a horizontal or vertical line.

Construct the perpendicular through $P$ to $g$.Reflection point over a lineĪs you can see, you can construct this quite easily on paper: You have a point \(P = (x,y)\) and a line \(g(x) = m \cdot x + t\) and you want to get the point \(P' = (x', y')\) that got mirrored over \(g\).

LINE REFLECTION GRAPH HOW TO
It's astonishing how difficult it is to find a good explanation how to reflect a point over a line that does not use higher math methods.


 0 kommentar(er)
0 kommentar(er)
